╥σΩ±≥
  ╤≥Γε≡σφφ  ≥σΩ±≥│Γ │ ∩≡εΓσΣσφφ  εß≈Φ±δσφⁿ
   
  ╬ß'║Ω≥:
  • ╥σΩ±≥
 

  Σα║ ∞εµδΦΓ│±≥ⁿ ±≥Γε≡■Γα≥Φ ΣΦφα∞│≈φ│ ≥σΩ±≥Φ. ╥αΩ│ ≥σΩ±≥Φ ∞εµ≤≥ⁿ ∞│±≥Φ≥Φ εß≈Φ±δσφφ ,  Ω│ αΓ≥ε∞α≥Φ≈φε ∩≡Φ±≥ε±εΓ≤■≥ⁿ±  Σε ≡≤⌡≤ εß'║Ω≥│Γ.

▀Ω∙ε φα≥Φ±φ≤≥Φ ∞Φ°Ωε■ φα TσΩ±≥ , Γ│ΣΩ≡ΦΓα║≥ⁿ±  Σ│αδεπεΓσ Γ│Ωφε ≥σΩ±≥≤. ▀Ω∙ε ταΩ≡Φ≥Φ Σ│αδεπεΓσ Γ│Ωφε, α ±Φ∞Γεδ ταδΦ°Φ≥Φ ∩ετφα≈σφΦ∞, ≥ε ≥σΩ±≥ ∞εµσ Γ│ΣΩ≡ΦΓα≥Φ±ⁿ φα≥Φ±Ωε∞ ∞Φ°ΩΦ φα ≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│.

 

─│αδεπεΓσ Γ│Ωφε ≥σΩ±≥≤


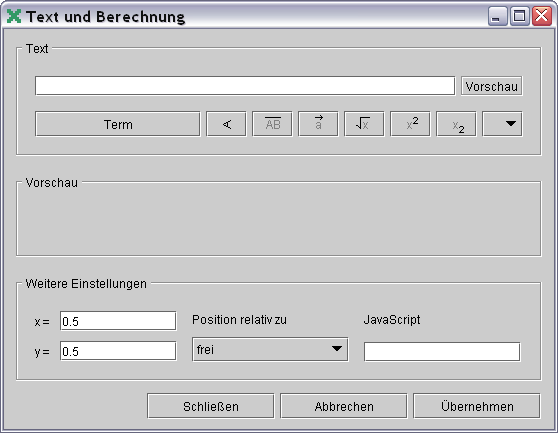
┬ΓσΣσφφ  ≥σΩ±≥≤ ∩≡εΓεΣΦ≥ⁿ±  ≈σ≡στ ∩εδσ ΓΓεΣ≤ ΣαφΦ⌡. ╙ Γ│Ωφ│ "╧ε∩σ≡σΣφ│Θ ∩σ≡σπδ Σ" Σσ∞εφ±≥≡≤║≥ⁿ±  ≥Φ∞≈α±εΓΦΘ Γα≡│αφ≥ ≥σΩ±≥≤ αßε ΓΦΣα║≥ⁿ±  ∩εΓ│Σε∞δσφφ  ∩≡ε ∩ε∞ΦδΩ≤. ╧ε≈α≥εΩ ≥σΩ±≥≤ φα ≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│ ∞εµφα ταΣα≥Φ ≈σ≡στ "x =" ≥α "y =". ▀Ω∙ε ∩≡Φ "╧ετΦ÷│  Γ│Σφε±φε Σε" ΣεΣα≥ΩεΓε ΓΦßΦ≡α║≥ⁿ±  τ ∩σ≡σδ│Ω≤ εß'║Ω≥, ≥ε ≥σΩ±≥ ≡≤⌡α║≥ⁿ±  Γ│Σφε±φε ÷ⁿεπε εß'║Ω≥α. ┬ ÷ⁿε∞≤ ΓΦ∩αΣΩ≤ ∩εΩατφΦΩΦ ∩ετΦ÷│┐ ≥σΩ±≥≤ ║ ≥αΩεµ Γ│Σφε±φΦ∞Φ .
 

┬ ±≥αφ│ ╨≤⌡α≥Φ ∞εµφα ∩σ≡σ∞│∙≤Γα≥Φ ≥σΩ±≥Φ.
┬  Σ│αδεπεΓε∞≤ Γ│Ωφ│ ┬δα±≥ΦΓε±≥│ εß'║Ω≥α ∞εµφα τ∞│φ■Γα≥Φ ≥σΩ±≥Φ. ╥≤≥ µσ ∞εµφα τ∞│φ■Γα≥Φ ∩ετΦ÷│■ ≥σΩ±≥α, φα≥Φ±Ω≤■≈Φ φα "╥σΩ±≥ φσ≡≤⌡ε∞ΦΘ" αßε Γ ∩σ≡σδ│Ω≤ "╥ε≈φ│±≥ⁿ" Γ∩δΦΓα≥Φ φα ≈Φ±δε ≡ετ≡ Σ│Γ ∩│±δ  Ωε∞Φ ∩≡Φ εß≈Φ±δσφφ ⌡ Γ ≥σΩ±≥│ ( ╬ß≈Φ±δσφφ ) .


┬ΓσΣσφφ  ≥σΩ±≥≤

╩ε∞αφΣΦ τ <xyz>...</xyz> ∞εµ≤≥ⁿ ∩≡εΓεΣΦ≥Φ±ⁿ ≥│δⁿΩΦ ∩ε ≈σ≡τ│, α φσ ∩σ≡σ⌡≡σ±φε ≈Φ  Ω εΣφα Ωε∞αφΣα, ∙ε ΓΩδ■≈α║ │φ°│.

 

╤≤÷│δⁿφΦΘ ≥σΩ±≥

┬ΓσΣσφφ 

  • ≥σΩ±≥
text ∞εµσ ∞α≥Φ ß≤ΩΓσφ│ ≥α ÷Φ⌠≡εΓ│ τφαΩΦ.

╧≡ΦΩδαΣ:

  • ╓σ ≥σΩ±≥!

 

╬ß≈Φ±δσφφ 

┬ΓσΣσφφ 

  • <value>εß≈Φ±δσφφ </value>

╬ß≈Φ±δσφφ   ∩≡εΓεΣ ≥ⁿ±  Γ ∞σµα⌡ Ωε∞αφΣΦ value. ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│  ∞│±≥Φ≥ⁿ±  Γ ≡ετΣ│δ│ ╧≡αΓΦδα εß≈Φ±δσφⁿ.
─≤µΩΦ value ΓΓεΣ ≥ⁿ±  ÷│║■ Ωφε∩Ωε■:

╧≡ΦΩδαΣΦ:

  • <value>Dist(A,B)</value> ║, φα∩≡ΦΩδαΣ, 3.25
  • ┬│ΣΣαδⁿ ±ΩδαΣα║ <value>Dist(A,B)</value>! ║, φα∩≡ΦΩδαΣ,  Γ│ΣΣαδⁿ ±ΩδαΣα║ 3.25!

 

╤Φ∞Γεδ Ω≤≥α

┬ΓσΣσφφ 

  • <arc>

╟φαΩε∞ <arc> ΓΓεΣΦ≥ⁿ±  ∞αδσφⁿΩα Σ≤πα Ω≤≥α.

<arc> ∞εµσ ΓΓεΣΦ≥Φ±ⁿ ÷│║■ Ωφε∩Ωε■:

 

╨Φ±Ωα φαΣ ß≤ΩΓε■

┬ΓσΣσφφ 

  • <overline>≥σΩ±≥</overline>

═αΣ ≥σΩ±≥ ∩≡εΓεΣΦ≥ⁿ±  ≡Φ±Ωα.

─≤µΩΦ overline ΓΓεΣ ≥ⁿ±  ÷│║■ Ωφε∩Ωε■:

╧≡ΦΩδαΣ:

  • <overline>AB</overline> ετφα≈α║ ΣεΓµΦφ≤ Γ│Σ≡│τΩα [AB]

 

╤≥≡│δΩα

┬ΓσΣσφφ 

  • <arrow>text</arrow>

═αΣ ≥σΩ±≥ ∩≡εΓεΣΦ≥ⁿ±  ±≥≡│δΩα.

─≤µΩΦ arrow ΓΓεΣ ≥ⁿ±  ÷│║■ Ωφε∩Ωε■:

╧≡ΦΩδαΣ:

  • <arrow>a</arrow> ∩≡εΓεΣΦ≥ⁿ ∞αδσφⁿΩ≤ ±≥≡│δΩ≤ φαΣ a

 

╨αΣΦΩαδ

┬ΓσΣσφφ 

  • <sqrt>≥σΩ±≥</sqrt>

text ∩│Σ±≥αΓδ ║≥ⁿ±  ∩│Σ ≡αΣΦΩαδ.

─≤µΩΦ sqrt ΓΓεΣ ≥ⁿ±  ÷│║■ Ωφε∩Ωε■:

╧≡ΦΩδαΣ:

  • <sqrt>2</sqrt> ∞αδ■║ ≡αΣΦΩαδ φαΣ 2

 

═αΣ≡ ΣΩεΓΦΘ ≥σΩ±≥

┬ΓσΣσφφ 

  • ^z
  • ^{≥σΩ±≥}

╙ ∩σ≡°ε∞≤ ΓΦ∩αΣΩ≤ z  Ω εΩ≡σ∞ΦΘ ±Φ∞Γεδ ±≥αΓΦ≥ⁿ±  Γπε≡│. ═α Γ±│ │φ°│ ∩εΩατφΦΩΦ ÷σ φσ Γ∩δΦΓα║. ▀Ω∙ε ∩ε≥≡│ßφε ∩│Σφ ≥Φ ΣσΩ│δⁿΩα ±Φ∞Γεδ│Γ, ┐⌡ ±δ│Σ τα∩Φ±α≥Φ Γ Σ≤µΩα⌡ {}.

^{} ΓΓεΣ ≥ⁿ±  ÷│║■ Ωφε∩Ωε■:

╧≡ΦΩδαΣΦ:

  • x^2 Ω≡σ±δΦ≥ⁿ x τ φαΣ≡ ΣΩεΓΦ∞ ±Φ∞Γεδε∞ 2
  • x^{20} Ω≡σ±δΦ≥ⁿ x τ φαΣ≡ ΣΩεΓΦ∞ ±Φ∞Γεδε∞ 20

 

 

╧│Σ≡ ΣΩεΓΦΘ ≥σΩ±≥

┬ΓσΣσφφ 

  • _z
  • _{≥σΩ±≥}
╙ ∩σ≡°ε∞≤ ΓΦ∩αΣΩ≤  z   Ω εΩ≡σ∞ΦΘ ±Φ∞Γεδ ε∩≤±Ωα║≥ⁿ±  ΓφΦτ. ╓σ φσ Γ∩δΦΓα║ φα │φ°│ ∩εΩατφΦΩΦ. ▀Ω∙ε φσεß⌡│Σφε ε∩≤±≥Φ≥Φ ΓφΦτ ΣσΩ│δⁿΩα ±Φ∞Γεδ│Γ, ∩ε≥≡│ßφε ±Ωε≡Φ±≥α≥Φ±ⁿ Σ≡≤πΦ∞ Γα≡│αφ≥ε∞ τα∩Φ±≤ Γ Σ≤µΩα⌡ {}.

_{} ΓΓεΣ ≥ⁿ±  ÷│║■ Ωφε∩Ωε■:

╧≡ΦΩδαΣΦ:

  • P_2 τα∩Φ±≤║ P τ │φΣσΩ±ε∞ 2
  • P_{20} τα∩Φ±≤║ P τ │φΣσΩ±ε∞ 20

╤∩σ÷│αδⁿφ│ ±Φ∞ΓεδΦ

┬ΓσΣσφφ 

  • &±∩σ÷│αδⁿφ│ ±Φ∞ΓεδΦ;

▀Ω ±∩σ÷│αδⁿφ│ ±Φ∞ΓεδΦ    ΓΦΩε≡Φ±≥εΓ≤║ ∞αδσφⁿΩ│ π≡σ÷ⁿΩ│ δ│≥σ≡Φ. ─δ  ±∩σ÷│αδⁿφΦ⌡ ±Φ∞Γεδ│Γ ∞εµφα ß≡α≥Φ │∞σφα alpha, beta, ..., omega.

&±∩σ÷│αδⁿφΦΘ ±Φ∞Γεδ; ∞εµσ ΓΓεΣΦ≥Φ±ⁿ ÷│║■ Ωφε∩Ωε■:

╧≡ΦΩδαΣ:

  • &alpha; τα∩Φ±≤║ ∞αδσφⁿΩ≤ δ│≥σ≡≤ αδⁿ⌠α

 

─ε ∩ε≈α≥Ω≤ ±≥ε≡│φΩΦ

 
 
─ΦΓ. ≥αΩεµ: